概率初步(续)
概率初步(续)
- 条件概率公式
$$ P(B \mid A)=\frac{P(B \cap A)}{P(A)} $$
$$ P(B \cap A)=P(A) P(B \mid A) $$
- 全概率公式
$$ P(A)=\sum_{k=1}^n P\left(A \mid \Omega_k\right) P\left(\Omega_k\right) $$
- 分布的形式
$$ \left(\begin{array}{} x_1 & x_2 & \cdots & x_n \\ p_1 & p_2 & \cdots & p_n \end{array}\right) $$
- 设随机变量 $X$ 的分布如上, 那么其期望定义为
$$ E[X]=x_1 p_1+x_2 p_2+\cdots+x_n p_n $$
其方差定义为 $$ D[X]=E\left[(X-E[X])^2\right]=E\left[X^2\right]-(E[X])^2 $$
- 期望的线性性质
- (1) 如果 $X$ 是一个随机变量, $a$ 是一个实数, 那么
$$ E[a X + b]=a E[X] + b $$
- (2) 如果 $X 、 Y$ 是两个随机变量, 那么
$$ E[X+Y]=E[X]+E[Y] $$
- 方差的性质
- (1) 如果 $X$ 是一个随机变量, $a$ 是一个实数, 那么
$$ D[a X + b]=a ^2 D[X] $$
- (2) 如果 $X 、 Y$ 是两个独立的随机试验所对应的随机变量, 那么
$$ D[X+Y]=D[X]+D[Y] $$
- 二项分布: 独立地重复一个成功概率为 $p$ 的伯努利试验 $n$ 次, $X$ 表示成功次数, 那么 $X$ 的分布为二项分布.
$$ P(X=k)=C_n^k p^k(1-p)^{n-k},\space k=0,1,2, \cdots, n $$
$$ \left(\begin{array}{} 0 & 1 & 2 & \cdots & k & \cdots & n \\ q^n & \mathrm{C}_n^1 p q^{n-1} & \mathrm{C}_n^2 p^2 q^{n-2} & \cdots & \mathrm{C}_n^k p^k q^{n-k} & \cdots & p^n \end{array}\right) $$
- 从这个角度可以证明二项式定理
$$ \sum_{k=0}^n C_n^k p^k q^{n-k}=\sum_{k=0}^n P(X=k)=1 $$
- $ X \sim B\left(n, p\right)$ 即为 $X$服从成功 $n$ 次,成功概率为 $p$ 的二项分布
- $E[X]=n p, D[X]=np(1-p)$
- 超几何分布: 从一个装有大小与质地相同的 $a$ 个白球、 $b$ 个黑球的袋子中依次随机 且不放回地取 $n$ 个球. 用 $X$ 表示其中白球的个数, 则 $X$ 的分布称为超几何分布.
$$ P(X=k)=\frac{C_a^k C_b^{n-k}}{C_{a+b}^n} $$
$$ E[X]=\frac{n a}{a+b} $$
$$ D[X] = n\frac{a * b * (a+b-n)}{(a+b)^2 (a+b-1)} $$
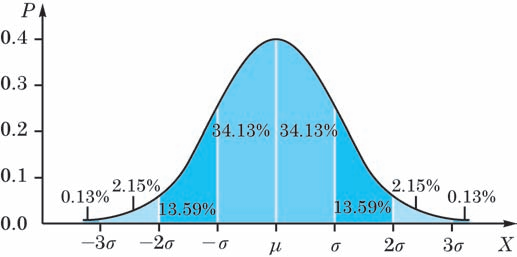
- 正态分布: 由钟形曲线
$$ \varphi_{\mu, \sigma^2}(x)=\frac{1}{\sqrt{2 \pi \sigma^2}} \mathrm{e}^{-\frac{(x-\mu)^2}{2 \sigma^2}},-\infty<x<+\infty $$
- 标准正态分布密度函数
$$ y=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{x^2}{2}} $$
- $y=\Phi(a)$ = $p(x < a)$ 为 从 $-\infty$ 到 $x = a$ 的累计面积
- $\Phi(-x) = 1 - \Phi(x)$
$$ X \sim N\left(\mu, \sigma^2\right) \to \frac{X-\mu}{\sigma} \sim N(0,1) $$
- $E[x] = \mu , D[x] = \sigma^2$